Normal Mode Analysis

Perform elastic network model (ENM) C-alpha normal modes calculation of a protein structure.

# S3 method for pdb
nma(pdb, inds = NULL, ff = 'calpha', pfc.fun = NULL,
                  mass = TRUE, temp = 300.0, keep = NULL, hessian = NULL,
                  outmodes = NULL, ... )

build.hessian(xyz, pfc.fun, fc.weights = NULL, pdb = NULL, ...)

# S3 method for nma
print(x, nmodes=6, ...)

Arguments

pdb	an object of class `pdb` as obtained from function `read.pdb`.
inds	atom and xyz coordinate indices obtained from `atom.select` that selects the elements of `pdb` upon which the calculation should be based. If not provided the function will attempt to select the calpha atoms automatically (based on function `atom.select`).
ff	character string specifying the force field to use: ‘calpha’, ‘anm’, ‘pfanm’, ‘reach’, or ‘sdenm’.
pfc.fun	customized pair force constant (‘pfc’) function. The provided function should take a vector of distances as an argument to return a vector of force constants. If provided, 'pfc.fun' will override argument `ff`. See examples below.
mass	logical, if TRUE the Hessian will be mass-weighted.
temp	numerical, temperature for which the amplitudes for scaling the atomic displacement vectors are calculated. Set ‘temp=NULL’ to avoid scaling.
keep	numerical, final number of modes to be stored. Note that all subsequent analyses are limited to this subset of modes. This option is useful for very large structures and cases where memory may be limiting.
hessian	hessian matrix as obtained from `build.hessian`. For internal purposes and generally not intended for public use.
outmodes	atom indices as obtained from `atom.select`) specifying the atoms to include in the resulting mode object.
xyz	a numeric vector of Cartesian coordinates.
fc.weights	a numeric matrix of size NxN (where N is the number of calpha atoms) containg scaling factors for the pariwise force constants. See examples below.
x	an `nma` object obtained from `nma.pdb`.
nmodes	numeric, number of modes to be printed.
...	additional arguments to `build.hessian`, `aa2mass`, `pfc.fun`, and `print`. One useful option here for dealing with unconventional residues is ‘mass.custom’, see the `aa2mass` function for details.

Details

This function calculates the normal modes of a C-alpha model of a protein structure. A number of force fields are implemented all of whhich employ the elastic network model (ENM).

The ‘calpha’ force field - originally developed by Konrad Hinsen - is the recommended one for most applications. It employs a spring force constant differentiating between nearest-neighbour pairs along the backbone and all other pairs. The force constant function was parameterized by fitting to a local minimum of a crambin model using the AMBER94 force field.

See load.enmff for details of the different force fields.

By default nma.pdb will diagonalize the mass-weighted Hessian matrix. The resulting mode vectors are moreover scaled by the thermal fluctuation amplitudes.

The implementation under default arguments reproduces the calculation of normal modes (VibrationalModes) in the Molecular Modeling Toolkit (MMTK) package. To reproduce ANM modes set ff='anm', mass=FALSE, and temp=NULL.

Value

Returns an object of class ‘nma’ with the following components:

modes

numeric matrix with columns containing the normal mode vectors. Mode vectors are converted to unweighted Cartesian coordinates when mass=TRUE. Note that the 6 first trivial eigenvectos appear in columns one to six.

frequencies

numeric vector containing the vibrational frequencies corresponding to each mode (for mass=TRUE).

force.constants

numeric vector containing the force constants corresponding to each mode (for mass=FALSE)).

fluctuations

numeric vector of atomic fluctuations.

numeric matrix with columns containing the raw eigenvectors. Equals to the modes component when mass=FALSE and temp=NULL.

numeric vector containing the raw eigenvalues.

xyz

numeric matrix of class xyz containing the Cartesian coordinates in which the calculation was performed.

mass

numeric vector containing the residue masses used for the mass-weighting.

temp

numerical, temperature for which the amplitudes for scaling the atomic displacement vectors are calculated.

triv.modes

number of trivial modes.

natoms

number of C-alpha atoms.

call

the matched call.

Note

The current version provides an efficent implementation of NMA with execution time comparable to similar software (when the entire Hessian is diagonalized).

The main (speed related) bottleneck is currently the diagonalization of the Hessian matrix which is performed with the core R function eigen. For computing a few (5-20) approximate modes the user can consult package ‘irlba’.

NMA is memory extensive and users should be cautions when running larger proteins (>3000 residues). Use ‘keep’ to reduce the amount of memory needed to store the final ‘nma’ object (the full 3Nx3N Hessian matrix still needs to be allocated).

We thank Edvin Fuglebakk for valuable discussions on the implementation as well as for contributing with testing.

References

Skjaerven, L. et al. (2014) BMC Bioinformatics 15, 399. Grant, B.J. et al. (2006) Bioinformatics 22, 2695--2696. Hinsen, K. et al. (2000) Chemical Physics 261, 25--37.

Author

Lars Skjaerven

Examples

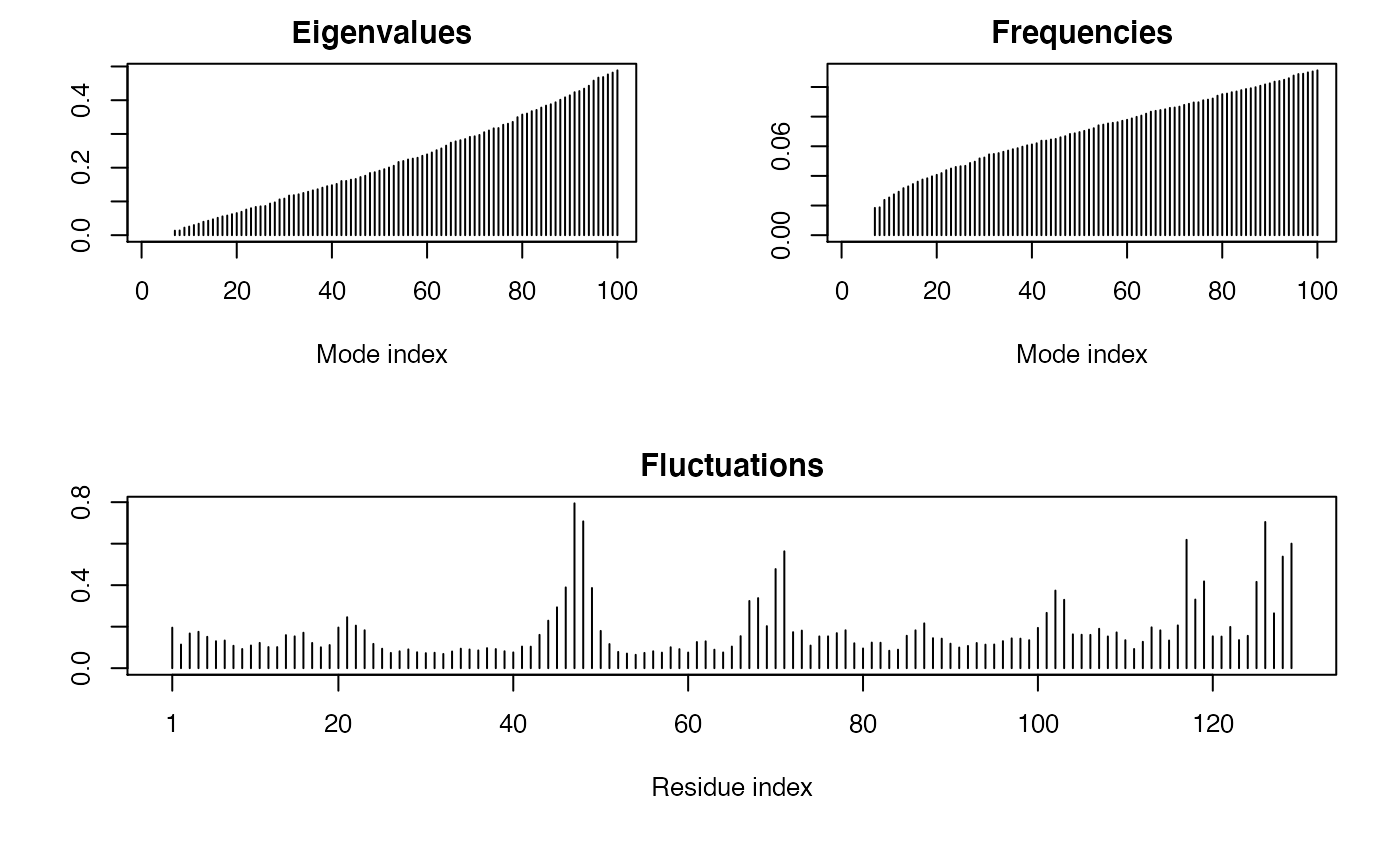
## Fetch stucture
pdb <- read.pdb( system.file("examples/1hel.pdb", package="bio3d") )

## Calculate normal modes
modes <- nma(pdb)
#>  Building Hessian...		Done in 0.012 seconds.
#>  Diagonalizing Hessian...	Done in 0.076 seconds.

## Print modes
print(modes)
#> 
#> Call:
#>   nma.pdb(pdb = pdb)
#> 
#> Class:
#>   VibrationalModes (nma)
#> 
#> Number of modes:
#>   387 (6 trivial)
#> 
#> Frequencies:
#>   Mode 7: 	0.018
#>   Mode 8: 	0.019
#>   Mode 9: 	0.024
#>   Mode 10: 	0.025
#>   Mode 11: 	0.028
#>   Mode 12: 	0.029
#> 
#> + attr: modes, frequencies, force.constants, fluctuations,
#>         U, L, xyz, mass, temp, triv.modes, natoms, call

## Plot modes
plot(modes)

## Visualize modes
#m7 <- mktrj.nma(modes, mode=7, file="mode_7.pdb")

if (FALSE) {
## Use Anisotropic Network Model
modes <- nma(pdb, ff="anm", mass=FALSE, temp=NULL, cutoff=15)

## Use SSE information and SS-bonds
sse      <- dssp(pdb, resno=FALSE, full=TRUE)
ss.bonds <- matrix(c(76,94, 64,80, 30,115, 6,127),
                   ncol=2, byrow=TRUE)


## User defined energy function
## Note: Must take a vector of distances
"my.ff" <- function(r) {
   ifelse( r>15, 0, 1 )
}

## Modes with a user defined energy function
modes <- nma(pdb, pfc.fun=my.ff)


## A more manual approach
sele <- atom.select(pdb, chain='A', elety='CA')
xyz <- pdb$xyz[sele$xyz]

hessian <- build.hessian(xyz, my.ff)
modes <- eigen(hessian)

## Dealing with unconventional residues
pdb <- read.pdb("1xj0")

## nma(pdb)
#modes <- nma(pdb, mass.custom=list(CSX=121.166))
}