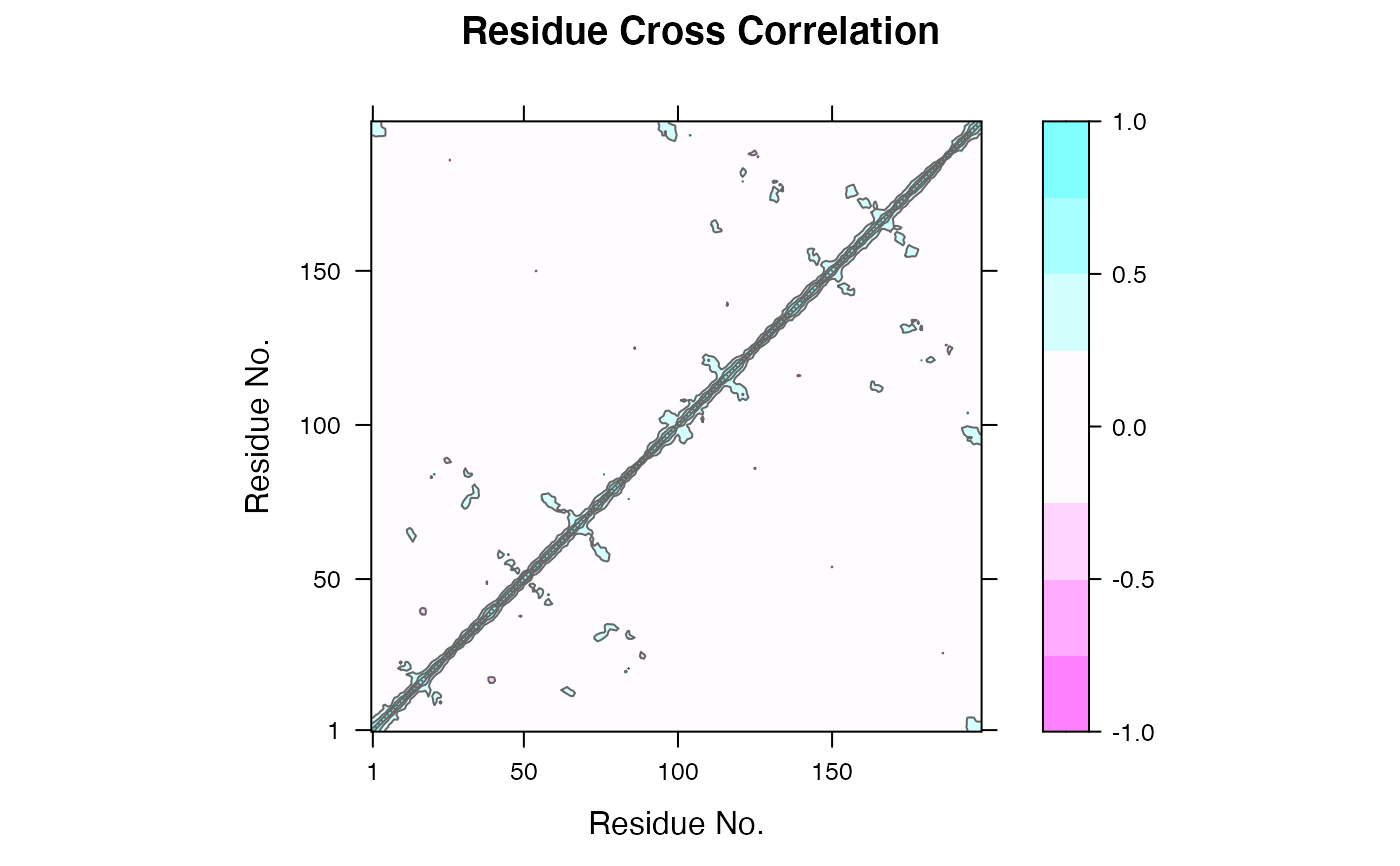
Dynamical Cross-Correlation Matrix from Principal Component Analysis
dccm.pca.RdCalculate the cross-correlation matrix from principal component analysis (PCA).
# S3 method for pca dccm(x, pc = NULL, method = c("pearson", "lmi"), ncore = NULL, ...)
Arguments
| x | an object of class |
|---|---|
| pc | numerical, indices of PCs to be included in the calculation.
If all negative, PCs complementary to |
| method | method to calculate the cross-correlation. Currently supports Pearson and linear mutual information (LMI). |
| ncore | number of CPU cores used to do the calculation.
By default ( |
| ... | Additional arguments to be passed (currently ignored). |
Details
This function calculates the cross-correlation matrix from principal
component analysis (PCA) obtained from pca.xyz of a set of protein
structures. It is an alternative way to calculate correlation in addition
to the conventional way from xyz coordinates directly. But, in this new
way one can freely chooses the PCs to be included in the
calculation (e.g. for filtering out PCs with small eigenvalues).
Value
Returns a cross-correlation matrix with values in a range from -1 to 1 (Pearson) or from 0 to 1 (LMI).
References
Grant, B.J. et al. (2006) Bioinformatics 22, 2695--2696.
Author
Xin-Qiu Yao
See also
Examples
# \donttest{ ##-- Read example trajectory file trtfile <- system.file("examples/hivp.dcd", package="bio3d") trj <- read.dcd(trtfile)#> Warning: truncating string with embedded nuls#> Warning: truncating string with embedded nuls#> NATOM = 198 #> NFRAME= 117 #> ISTART= 0 #> last = 117 #> nstep = 117 #> nfile = 117 #> NSAVE = 1 #> NDEGF = 0 #> version 24 #> Reading (x100) | | | 0% | |= | 1% | |= | 2% | |== | 3% | |=== | 4% | |==== | 5% | |==== | 6% | |===== | 7% | |===== | 8% | |====== | 9% | |======= | 9% | |======= | 10% | |======== | 11% | |======== | 12% | |========= | 13% | |========== | 14% | |========== | 15% | |=========== | 16% | |============ | 17% | |============= | 18% | |============= | 19% | |============== | 20% | |============== | 21% | |=============== | 22% | |================ | 22% | |================ | 23% | |================= | 24% | |================== | 25% | |================== | 26% | |=================== | 27% | |=================== | 28% | |==================== | 28% | |===================== | 29% | |===================== | 30% | |====================== | 31% | |====================== | 32% | |======================= | 33% | |======================== | 34% | |========================= | 35% | |========================= | 36% | |========================== | 37% | |=========================== | 38% | |=========================== | 39% | |============================ | 40% | |============================ | 41% | |============================= | 41% | |============================== | 42% | |============================== | 43% | |=============================== | 44% | |=============================== | 45% | |================================ | 46% | |================================= | 47% | |================================== | 48% | |================================== | 49% | |=================================== | 50% | |==================================== | 51% | |==================================== | 52% | |===================================== | 53% | |====================================== | 54% | |======================================= | 55% | |======================================= | 56% | |======================================== | 57% | |======================================== | 58% | |========================================= | 59% | |========================================== | 59% | |========================================== | 60% | |=========================================== | 61% | |=========================================== | 62% | |============================================ | 63% | |============================================= | 64% | |============================================= | 65% | |============================================== | 66% | |=============================================== | 67% | |================================================ | 68% | |================================================ | 69% | |================================================= | 70% | |================================================= | 71% | |================================================== | 72% | |=================================================== | 72% | |=================================================== | 73% | |==================================================== | 74% | |==================================================== | 75% | |===================================================== | 76% | |====================================================== | 77% | |====================================================== | 78% | |======================================================= | 78% | |======================================================== | 79% | |======================================================== | 80% | |========================================================= | 81% | |========================================================= | 82% | |========================================================== | 83% | |=========================================================== | 84% | |============================================================ | 85% | |============================================================ | 86% | |============================================================= | 87% | |============================================================== | 88% | |============================================================== | 89% | |=============================================================== | 90% | |=============================================================== | 91% | |================================================================ | 91% | |================================================================= | 92% | |================================================================= | 93% | |================================================================== | 94% | |================================================================== | 95% | |=================================================================== | 96% | |==================================================================== | 97% | |===================================================================== | 98% | |===================================================================== | 99% | |======================================================================| 100%## Read the starting PDB file to determine atom correspondence pdbfile <- system.file("examples/hivp.pdb", package="bio3d") pdb <- read.pdb(pdbfile) ## Select residues 24 to 27 and 85 to 90 in both chains inds <- atom.select(pdb, resno=c(24:27,85:90), elety='CA') ## lsq fit of trj on pdb xyz <- fit.xyz(pdb$xyz, trj, fixed.inds=inds$xyz, mobile.inds=inds$xyz) ## Do PCA pca <- pca.xyz(xyz) ## DCCM: only use first 10 PCs cij <- dccm(pca, pc = c(1:10)) ## Plot DCCM plot(cij)# }