Calculate Torsion/Dihedral Angles

Defined from the Cartesian coordinates of four successive atoms (A-B-C-D) the torsion or dihedral angle is calculated about an axis defined by the middle pair of atoms (B-C).

torsion.xyz(xyz, atm.inc = 4)

Arguments

xyz

a numeric vector of Cartisean coordinates.
atm.inc

a numeric value indicating the number of atoms to increment by between successive torsion evaluations (see below).

Details

The conformation of a polypeptide or nucleotide chain can be usefully described in terms of angles of internal rotation around its constituent bonds.

If a system of four atoms A-B-C-D is projected onto a plane normal to bond B-C, the angle between the projection of A-B and the projection of C-D is described as the torsion angle of A and D about bond B-C.

By convention angles are measured in the range -180 to +180, rather than from 0 to 360, with positive values defined to be in the clockwise direction.

With atm.inc=1, torsion angles are calculated for each set of four successive atoms contained in xyz (i.e. moving along one atom, or three elements of xyz, between sucessive evaluations). With atm.inc=4, torsion angles are calculated for each set of four successive non-overlapping atoms contained in xyz (i.e. moving along four atoms, or twelve elements of xyz, between sucessive evaluations).

Value

A numeric vector of torsion angles.

References

Grant, B.J. et al. (2006) Bioinformatics 22, 2695--2696.

Author

Karim ElSawy

Note

Contributions from Barry Grant.

See also

torsion.pdb, pca.tor, wrap.tor, read.pdb, read.dcd.

Examples


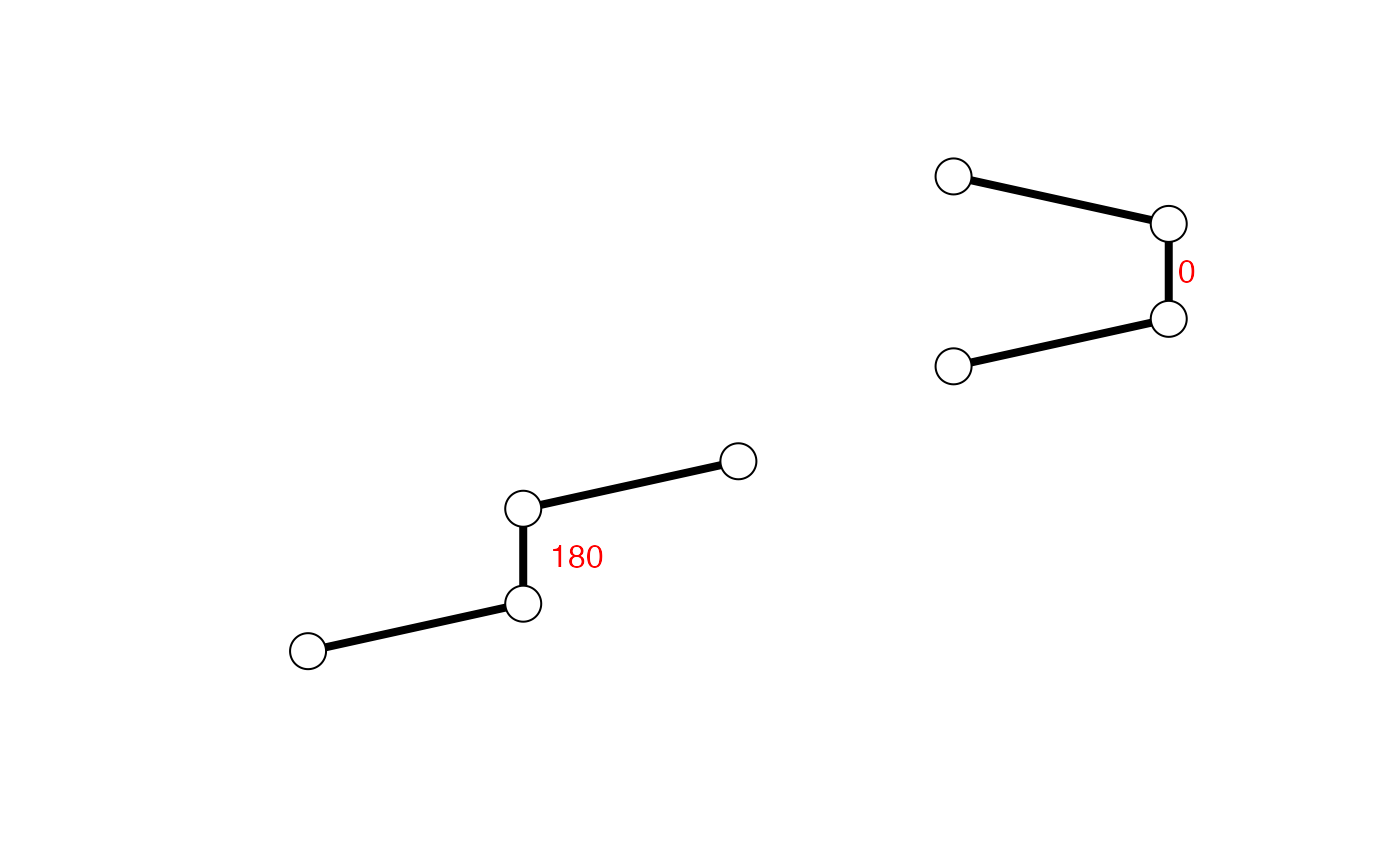
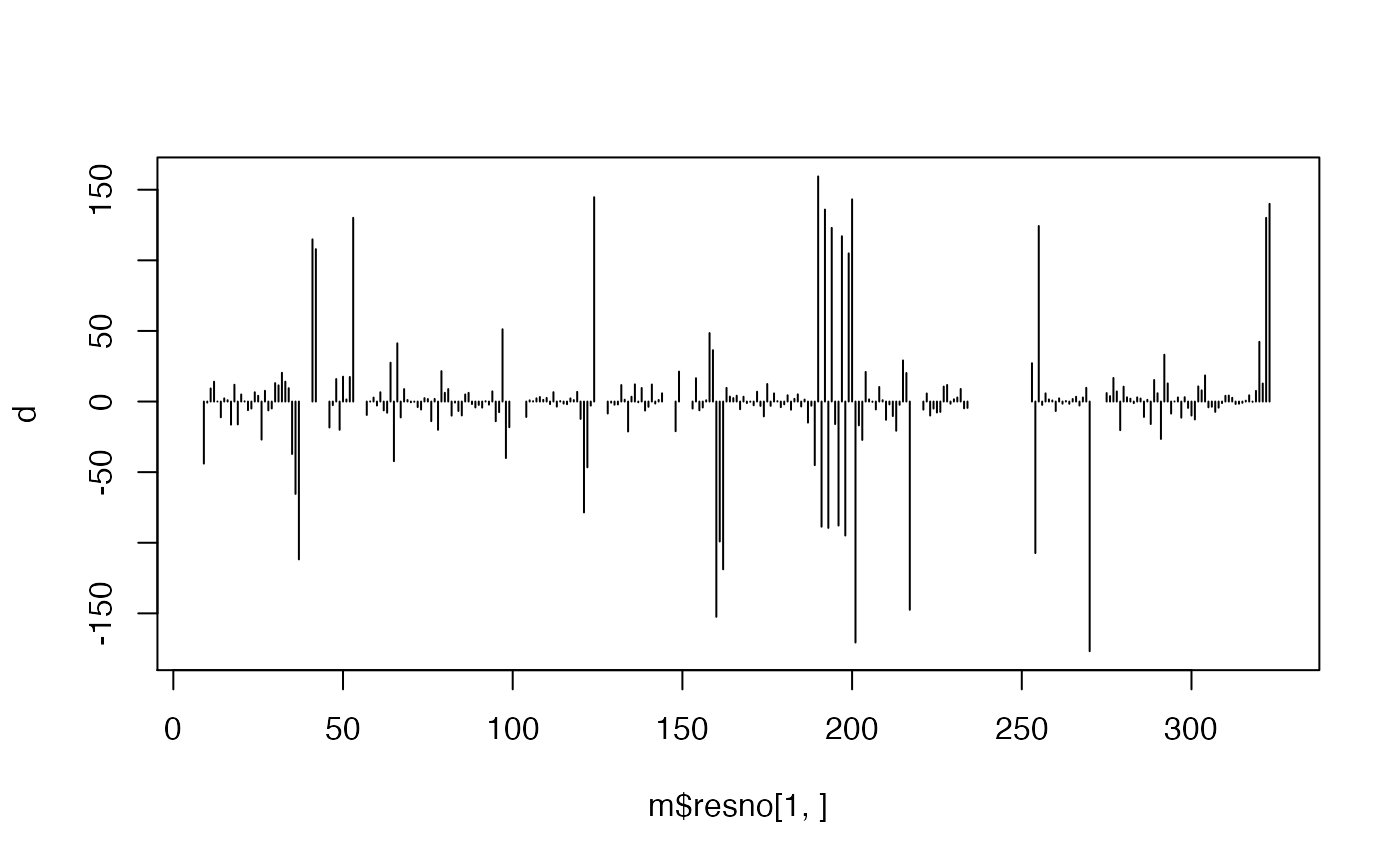
## Calculate torsions for cis & trans conformers
xyz <- rbind(c(0,-0.5,0,1,0,0,1,1,0,0,1.5,0),
             c(0,-0.5,0,1,0,0,1,1,0,2,1.5,0)-3)
cis.tor   <- torsion.xyz( xyz[1,] )
trans.tor <- torsion.xyz( xyz[2,] )
apply(xyz, 1, torsion.xyz)

#> [1]   0 180


plot(range(xyz), range(xyz), xlab="", ylab="", typ="n", axes=FALSE)

  apply(xyz, 1, function(x){
    lines(matrix(x, ncol=3, byrow=TRUE), lwd=4)
    points(matrix(x, ncol=3, byrow=TRUE), cex=2.5,
           bg="white", col="black", pch=21) } )

#> NULL
  
  text( t(apply(xyz, 1, function(x){
    apply(matrix(x, ncol=3, byrow=TRUE)[c(2,3),], 2, mean) })),
       labels=c(0,180), adj=-0.5, col="red")


# \donttest{
# PDB server connection required - testing excluded

##-- PDB torsion analysis
pdb <- read.pdb("1bg2")

#>   Note: Accessing on-line PDB file
#> Warning: /var/folders/xf/qznxnpf91vb1wm4xwgnbt0xr0000gn/T//Rtmp9oBdbc/1bg2.pdb  exists. Skipping download
tor <- torsion.pdb(pdb)
## basic Ramachandran plot
plot(tor$phi, tor$psi)


## torsion analysis of a single coordinate vector 
inds <- atom.select(pdb,"calpha")
tor.ca <- torsion.xyz(pdb$xyz[inds$xyz], atm.inc=3)

##-- Compare two PDBs to highlight interesting residues
aln <- read.fasta(system.file("examples/kif1a.fa",package="bio3d"))
m <- read.fasta.pdb(aln)

#> pdb/seq: 1   name: http://www.rcsb.org/pdb/files/1bg2.pdb 
#> pdb/seq: 2   name: http://www.rcsb.org/pdb/files/1i6i.pdb 
#>    PDB has ALT records, taking A only, rm.alt=TRUE
#> pdb/seq: 3   name: http://www.rcsb.org/pdb/files/1i5s.pdb 
#>    PDB has ALT records, taking A only, rm.alt=TRUE
#> pdb/seq: 4   name: http://www.rcsb.org/pdb/files/2ncd.pdb 
a <- torsion.xyz(m$xyz[1,],1)
b <- torsion.xyz(m$xyz[2,],1)
## Note the periodicity of torsion angles
d <- wrap.tor(a-b)
plot(m$resno[1,],d, typ="h")


# }