Calculate Mainchain and Sidechain Torsion/Dihedral Angles

Calculate all torsion angles for a given protein PDB structure object.

torsion.pdb(pdb)

Arguments

pdb	a PDB structure object as obtained from function `read.pdb`.

Details

The conformation of a polypeptide chain can be usefully described in terms of angles of internal rotation around its constituent bonds. See the related torsion.xyz function, which is called by this function, for details.

Value

Returns a list object with the following components:

phi

main chain torsion angle for atoms C,N,CA,C.

psi

main chain torsion angle for atoms N,CA,C,N.

omega

main chain torsion angle for atoms CA,C,N,CA.

alpha

virtual torsion angle between consecutive C-alpha atoms.

chi1

side chain torsion angle for atoms N,CA,CB,*G.

chi2

side chain torsion angle for atoms CA,CB,*G,*D.

chi3

side chain torsion angle for atoms CB,*G,*D,*E.

chi4

side chain torsion angle for atoms *G,*D,*E,*Z.

chi5

side chain torsion angle for atoms *D,*E,*Z, NH1.

coords

numeric matrix of ‘justified’ coordinates.

tbl

a numeric matrix of psi, phi and chi torsion angles.

References

Grant, B.J. et al. (2006) Bioinformatics 22, 2695--2696.

Author

Barry Grant

Note

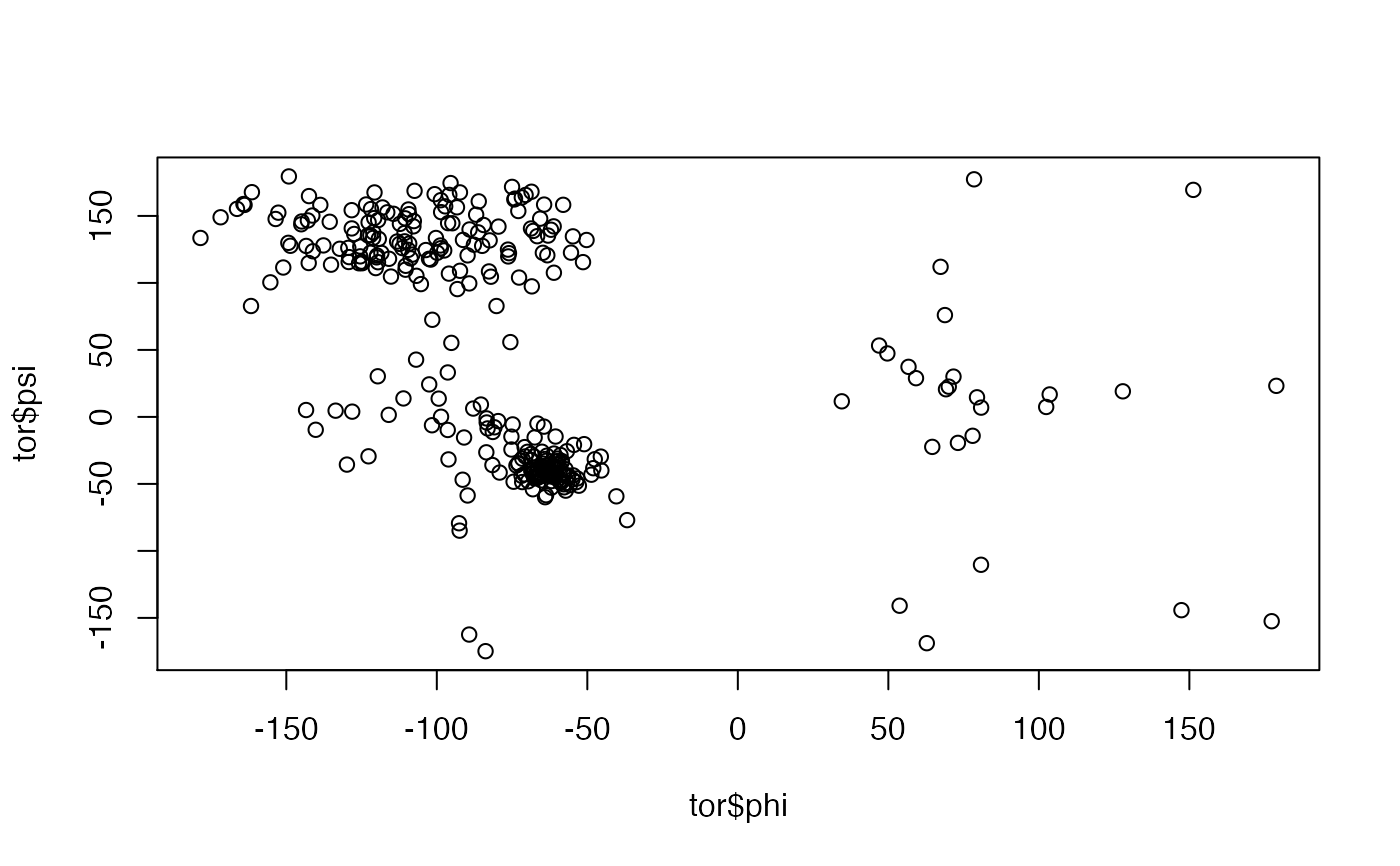
For the protein backbone, or main-chain atoms, the partial double-bond character of the peptide bond between ‘C=N’ atoms severely restricts internal rotations. In contrast, internal rotations around the single bonds between ‘N-CA’ and ‘CA-C’ are only restricted by potential steric collisions. Thus, to a good approximation, the backbone conformation of each residue in a given polypeptide chain can be characterised by the two angles phi and psi.

Sidechain conformations can also be described by angles of internal rotation denoted chi1 up to chi5 moving out along the sidechain.

Examples

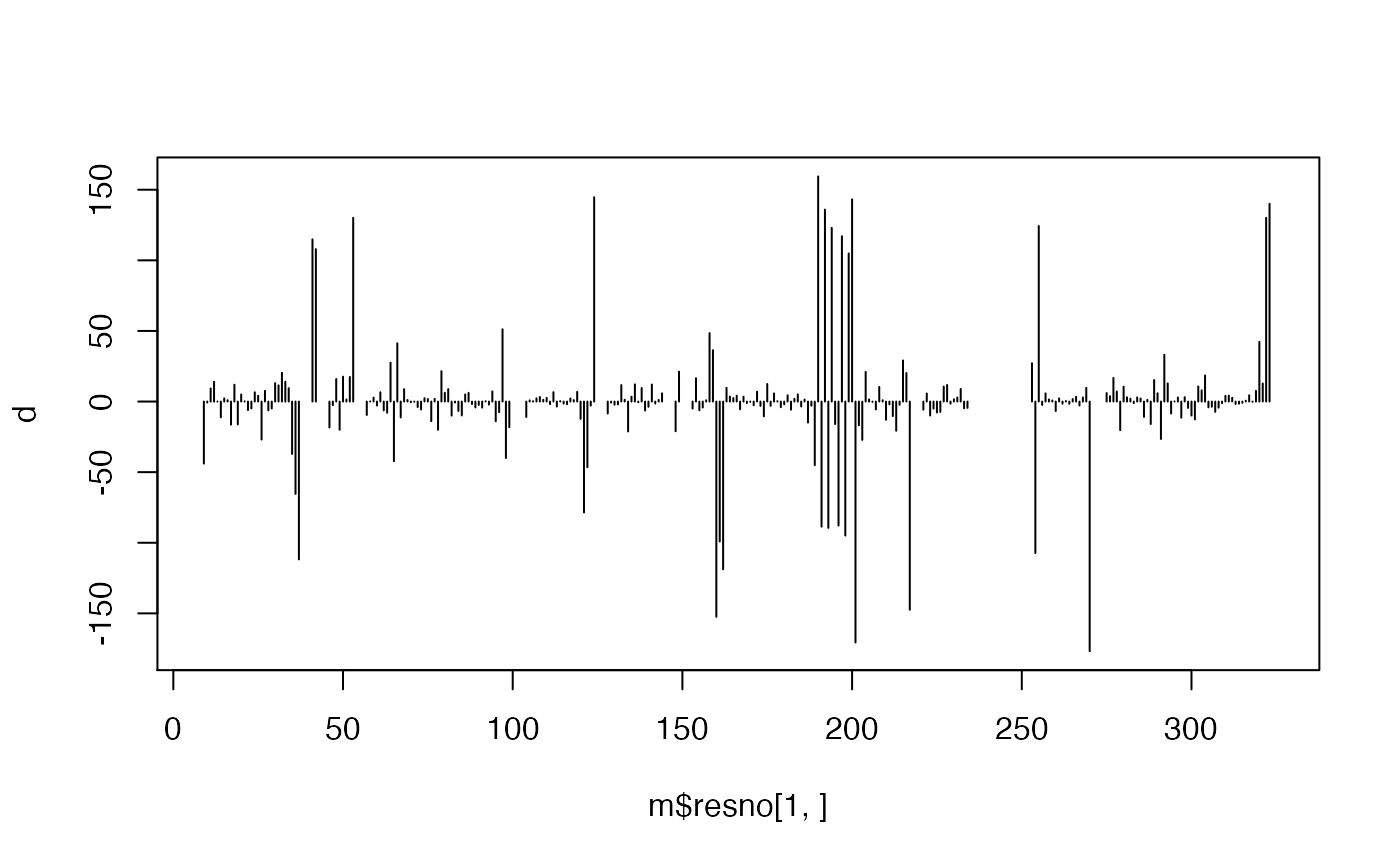
# \donttest{
# PDB server connection required - testing excluded

##-- PDB torsion analysis
pdb <- read.pdb( "1bg2" )
#>   Note: Accessing on-line PDB file
#> Warning: /var/folders/xf/qznxnpf91vb1wm4xwgnbt0xr0000gn/T//Rtmp9oBdbc/1bg2.pdb  exists. Skipping download
tor <- torsion.pdb(pdb)
head(tor$tbl)
#>                  phi        psi       chi1      chi2      chi3 chi4 chi5
#>   3.A.ASP         NA -21.550499  -45.13716 -47.35099        NA   NA   NA
#>   4.A.LEU  -64.02592 -59.916666  175.35429  58.11471        NA   NA   NA
#>   5.A.ALA -140.22879  -9.607914         NA        NA        NA   NA   NA
#>   6.A.GLU   67.34903 112.010164 -141.68005 -60.79993 -52.19896   NA   NA
#>   7.A.CYS   68.79209  76.000250  179.25704        NA        NA   NA   NA
#>   8.A.ASN  -95.17049  55.249681  -54.67200  29.83050        NA   NA   NA

## basic Ramachandran plot
plot(tor$phi, tor$psi)

## torsion analysis of a single coordinate vector 
#inds <- atom.select(pdb,"calpha")
#tor.ca <- torsion.xyz(pdb$xyz[inds$xyz], atm.inc=1)

##-- Compare two PDBs to highlight interesting residues
aln <- read.fasta(system.file("examples/kif1a.fa",package="bio3d"))
m <- read.fasta.pdb(aln)
#> pdb/seq: 1   name: http://www.rcsb.org/pdb/files/1bg2.pdb 
#> pdb/seq: 2   name: http://www.rcsb.org/pdb/files/1i6i.pdb 
#>    PDB has ALT records, taking A only, rm.alt=TRUE
#> pdb/seq: 3   name: http://www.rcsb.org/pdb/files/1i5s.pdb 
#>    PDB has ALT records, taking A only, rm.alt=TRUE
#> pdb/seq: 4   name: http://www.rcsb.org/pdb/files/2ncd.pdb 
a <- torsion.xyz(m$xyz[1,],1)
b <- torsion.xyz(m$xyz[2,],1)
d <- wrap.tor(a-b)
plot(m$resno[1,],d, typ="h")
# }