All Atom Normal Mode Analysis
Usage
aanma(...)"aanma"(pdb, pfc.fun = NULL, mass = TRUE, temp = 300, keep = NULL, hessian = NULL, outmodes = "calpha", rm.wat = TRUE, reduced = FALSE, rtb = FALSE, nmer = 1, ...)rtb(hessian, pdb, mass = TRUE, nmer = 1, verbose = TRUE)
Arguments
- ...
- additional arguments to
build.hessianandaa2mass. One useful option here for dealing with unconventional residues is ‘mass.custom’, see theaa2massfunction for details. - pdb
- an object of class
pdbas obtained from functionread.pdb. - pfc.fun
- customized pair force constant (‘pfc’) function. The provided function should take a vector of distances as an argument to return a vector of force constants. If NULL, the default function ‘aaenm2’ will be employed. (See details below).
- mass
- logical, if TRUE the Hessian will be mass-weighted.
- temp
- numerical, temperature for which the amplitudes for scaling the atomic displacement vectors are calculated. Set ‘temp=NULL’ to avoid scaling.
- keep
- numerical, final number of modes to be stored. Note that all subsequent analyses are limited to this subset of modes. This option is useful for very large structures and cases where memory may be limited.
- hessian
- hessian matrix as obtained from
build.hessian. For internal purposes and generally not intended for public use. - outmodes
- either a character (‘calpha’ or ‘noh’) or atom
indices as obtained from
atom.selectspecifying the atoms to include in the resulting mode object. (See details below). - rm.wat
- logical, if TRUE water molecules will be removed before calculation.
- reduced
- logical, if TRUE the coarse-grained (‘4-bead’) ENM will be employed. (See details below).
- rtb
- logical, if TRUE the rotation-translation block based approximate modes will be calculated. (See details below).
- nmer
- numerical, defines the number of residues per block (used only
when
rtb=TRUE). - verbose
- logical, if TRUE print detailed processing message
Value
-
Returns an object of class ‘nma’ with the following
components:
- modes
- numeric matrix with columns containing the normal mode
vectors. Mode vectors are converted to unweighted Cartesian
coordinates when
mass=TRUE. Note that the 6 first trivial eigenvectos appear in columns one to six. - frequencies
- numeric vector containing the vibrational
frequencies corresponding to each mode (for
mass=TRUE). - force.constants
- numeric vector containing the force constants
corresponding to each mode (for
mass=FALSE)). - fluctuations
- numeric vector of atomic fluctuations.
- U
- numeric matrix with columns containing the raw
eigenvectors. Equals to the
modescomponent whenmass=FALSEandtemp=NULL. - L
- numeric vector containing the raw eigenvalues.
- xyz
- numeric matrix of class
xyzcontaining the Cartesian coordinates in which the calculation was performed. - mass
- numeric vector containing the residue masses used for the mass-weighting.
- temp
- numerical, temperature for which the amplitudes for scaling the atomic displacement vectors are calculated.
- triv.modes
- number of trivial modes.
- natoms
- number of C-alpha atoms.
- call
- the matched call.
Description
Perform all-atom elastic network model normal modes calculation of a protein structure.
Details
This function builds an elastic network model (ENM) based on all
heavy atoms of input pdb, and performs subsequent normal mode
analysis (NMA) in various manners. By default, the ‘aaenm2’ force
field (defining of the spring constants between atoms) is used, which was
obtained by fitting to a local energy minimum of a crambin model
derived from the AMBER99SB force field. It employs a pair force constant
function which falls as r^-6, and specific force constants for
covalent and intra-residue atom pairs. See also load.enmff
for other force field options.
The outmodes argument controls the type of output modes. There are
two standard types of output modes: ‘noh’ and ‘calpha’.
outmodes='noh' invokes regular all-atom based ENM-NMA. When
outmodes='calpha', an effective Hessian with respect to all C-alpha
atoms will be first calculated using the same formula as in Hinsen et al.
NMA is then performed on this effective C-alpha based Hessian. In addition,
users can provide their own atom selection (see atom.select)
as the value of outmodes for customized output modes generation.
When reduced=TRUE, only a selection of all heavy atoms is used
to build the ENM. More specifically, three to five atoms per residue
constitute the model. Here the N, CA, C atoms represent the protein
backbone, and zero to two selected side chain atoms represent the side chain
(selected based on side chain size and the distance to CA). This
coarse-grained ENM has significantly improved computational efficiency and
similar prediction accuracy with respect to the all-atom ENM.
When rtb=TRUE, rotation-translation block (RTB) based approximate
modes will be calculated. In this method, each residue is assumed to be a
rigid body (or ‘block’) that has only rotational and translational
degrees of freedom. Intra-residue deformation is thus ignored.
(See Durand et al 1994 and Tama et al. 2000 for more details). N residues per
block is also supported, where N=1, 2, 3, etc. (See argument nmer).
The RTB method has significantly improved computational efficiency and
similar prediction accuracy with respect to the all-atom ENM.
By default the function will diagonalize the mass-weighted Hessian matrix. The resulting mode vectors are moreover scaled by the thermal fluctuation amplitudes.
References
Hinsen, K. et al. (2000) Chem. Phys. 261, 25. Durand, P. et al. (1994) Biopolymers 34, 759. Tama, F. et al. (2000) Proteins 41, 1.
Examples
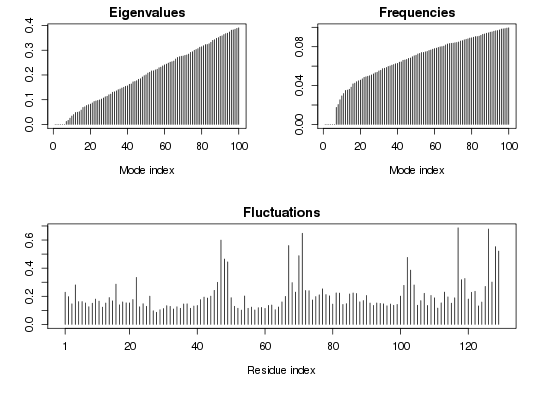
# All-atom NMA takes relatively long time - Don't run by default. ## Fetch stucture pdb <- read.pdb( system.file("examples/1hel.pdb", package="bio3d") ) ## Calculate all-atom normal modes modes.aa <- aanma(pdb, outmodes='noh')Building Hessian... Done in 1.539 seconds. Diagonalizing Hessian... Done in 55.844 seconds.## Calculate all-atom normal modes with RTB approximation modes.aa.rtb <- aanma(pdb, outmodes='noh', rtb=TRUE)Building Hessian... Done in 1.082 seconds. Diagonalizing Hessian with RTB... Done in 2.486 seconds.## Compare the two modes rmsip(modes.aa, modes.aa.rtb)$overlap b1 b2 b3 b4 b5 b6 b7 b8 b9 b10 a1 0.997 0.001 0.001 0 0.000 0.000 0.000 0.000 0.000 0.000 a2 0.002 0.962 0.034 0 0.001 0.000 0.000 0.000 0.000 0.000 a3 0.001 0.035 0.961 0 0.001 0.000 0.000 0.000 0.000 0.000 a4 0.000 0.000 0.000 1 0.000 0.000 0.000 0.000 0.000 0.000 a5 0.000 0.001 0.002 0 0.988 0.000 0.002 0.001 0.001 0.001 a6 0.000 0.000 0.000 0 0.000 0.999 0.000 0.001 0.000 0.000 a7 0.000 0.000 0.000 0 0.004 0.000 0.907 0.004 0.076 0.005 a8 0.000 0.000 0.000 0 0.001 0.001 0.006 0.981 0.000 0.008 a9 0.000 0.000 0.000 0 0.001 0.000 0.077 0.002 0.918 0.000 a10 0.000 0.000 0.000 0 0.000 0.000 0.004 0.010 0.001 0.979 $rmsip [1] 0.9989181 attr(,"class") [1] "rmsip"## Calculate C-alpha normal modes. modes <- aanma(pdb)Building Hessian... Done in 1.214 seconds. Extracting effective Hessian.. Done in 16.668 seconds. Diagonalizing Hessian... Done in 0.133 seconds.## Calculate C-alpha normal modes with reduced ENM. modes.cg <- aanma(pdb, reduced=TRUE)Building Hessian... Done in 0.438 seconds. Extracting effective Hessian.. Done in 2.729 seconds. Diagonalizing Hessian... Done in 0.132 seconds.## Calculate C-alpha normal modes with RTB approximation modes.rtb <- aanma(pdb, rtb=TRUE)Building Hessian... Done in 1.08 seconds. Extracting effective Hessian with RTB.. Done in 3.098 seconds. Diagonalizing Hessian with RTB... Done in 0.143 seconds.## Compare modes rmsip(modes, modes.cg)$overlap b1 b2 b3 b4 b5 b6 b7 b8 b9 b10 a1 0.977 0.005 0.000 0.000 0.002 0.001 0.001 0.001 0.001 0.000 a2 0.004 0.967 0.008 0.001 0.001 0.000 0.001 0.001 0.000 0.003 a3 0.001 0.007 0.936 0.013 0.008 0.001 0.008 0.000 0.000 0.000 a4 0.002 0.002 0.020 0.151 0.697 0.060 0.029 0.001 0.004 0.002 a5 0.000 0.000 0.006 0.654 0.219 0.015 0.041 0.000 0.004 0.001 a6 0.000 0.001 0.000 0.038 0.018 0.758 0.000 0.001 0.115 0.000 a7 0.002 0.000 0.001 0.080 0.011 0.004 0.625 0.014 0.173 0.009 a8 0.000 0.002 0.000 0.000 0.000 0.051 0.187 0.140 0.441 0.017 a9 0.001 0.000 0.001 0.009 0.000 0.019 0.012 0.658 0.126 0.005 a10 0.000 0.003 0.000 0.001 0.004 0.000 0.000 0.036 0.011 0.598 $rmsip [1] 0.9500757 attr(,"class") [1] "rmsip"rmsip(modes, modes.rtb)$overlap b1 b2 b3 b4 b5 b6 b7 b8 b9 b10 a1 1 0 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 a2 0 1 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.000 a3 0 0 0.996 0.003 0.000 0.000 0.000 0.000 0.000 0.000 a4 0 0 0.003 0.980 0.001 0.000 0.008 0.004 0.001 0.000 a5 0 0 0.000 0.001 0.998 0.000 0.000 0.000 0.000 0.000 a6 0 0 0.000 0.001 0.000 0.949 0.044 0.003 0.002 0.000 a7 0 0 0.000 0.011 0.000 0.049 0.833 0.097 0.007 0.000 a8 0 0 0.000 0.001 0.000 0.000 0.107 0.889 0.001 0.000 a9 0 0 0.000 0.000 0.000 0.001 0.006 0.003 0.987 0.000 a10 0 0 0.000 0.000 0.000 0.000 0.000 0.000 0.000 0.999 $rmsip [1] 0.99936 attr(,"class") [1] "rmsip"## Print modes print(modes)Call: aanma.pdb(pdb = pdb) Class: VibrationalModes (nma) Number of modes: 387 (6 trivial) Frequencies: Mode 7: 0.018 Mode 8: 0.021 Mode 9: 0.025 Mode 10: 0.029 Mode 11: 0.032 Mode 12: 0.035 + attr: modes, frequencies, force.constants, fluctuations, U, L, xyz, mass, temp, triv.modes, natoms, call## Plot modes plot(modes) ## Visualize modes #m7 <- mktrj.nma(modes, mode=7, file="mode_7.pdb", pdb=pdb)
See also
nma.pdb for C-alpha based NMA, aanma.pdbs for
ensemble all-atom NMA, load.enmff for available ENM force
fields, and fluct.nma, mktrj.nma, and
dccm.nma for various post-NMA calculations.